Pit Optimization Essentials
In addition to maximizing value, Studio NPVS also has options for creating an ultimate pit that maximizes the resource or meets blending requirements.
-
A fast implementation of the Pseudoflow algorithm is used to determine the ultimate pit for given prices, a set of cost parameters and engineering constraints such as wall slopes and pit limits.
-
The Ultimate Pit is a pit shell defining the economic limits of mining for the given deposit.
-
Nested LG Shells can be optionally computed.
-
Bench discounting from the existing topography can be applied when generating the ultimate pit and LG shells.
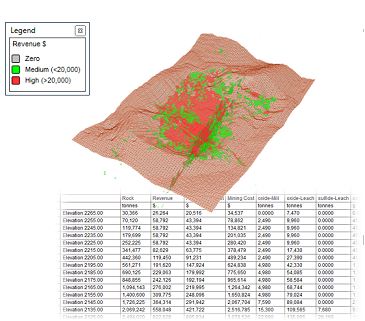
Ultimate pit wireframe
showing relationship to revenue distribution
Lexicon of terms
-
Pseudoflow method – Mathematical algorithm belonging to the family of Network Flows methods that finds open pit shell yielding maximum profit.
-
Pseudoflow parametrization – Successive application of the LG method to a block model with varying block values (net profits from blocks). The block values can be modified (parametrized) directly (each block reference value is multiplied by a factor), through product prices (the gross revenue or the price less the selling cost are multiplied by a factor), or through mining costs (the mining costs are multiplied by a factor). For direct and price parametrizations, small positive fractional factors yield small pits with high grade ore; gradually increasing the factors produces a sequence of ever bigger pit shells. Typically, we start at 0.01 and go up by 0.01 until we reach 1.0; sometimes we continue beyond 1.0, for example up to 1.2. For mining costs parametrization, the pit size increases when the factor decreases; we may start with 2.0 and descend down to 1.0.
-
Ultimate Pit – A pit shell defining the limits to mining for the given deposit. In mining literature this term is sometimes synonymous with LG Ultimate Pit.
-
LG Ultimate Pit – Ultimate Pit obtained with the LG method.
-
Discounted Ultimate Pit – LG Ultimate Pit when the block values have been discounted by the [Top-Down] method.
-
Maximum Resource Pit – A pit that contains all ore that is mineable under given slope angles; can be generated with the LG method by setting all costs to zero.
-
Nested Pits – A sequence of pits where each pit, except for the first one, is an extension of the previous pit in the sequence.
-
LG Shells or LG Phases – Nested Pits generated by LG parametrization.
-
Optimal Extraction Sequence (OES) – A sequence of blocks that is mineable under given slope angles and optimized according to some criteria. Mining blocks in OES creates nested pits. The number of all possible nested pits equals the number of blocks in OES.
-
Blended OES – OES generating nested pits maintaining balance between elements or rock types according to user defined blending criteria.
-
Pit by Pit OES – OES generated with respect to a given sequence of nested pits according to the following principles. (1) OES mines the first pit, then the second, and so on until the last. (2) Within each pit blocks are mined bench by bench. (3) On each bench blocks are sorted according to their values and to follow the contiguous mining rule as close as possible.
-
Pit Optimizer OES – Pit by Pit OES with respect to LG Shells.
Using Boundaries
There are several options for controlling ultimate pit limits.
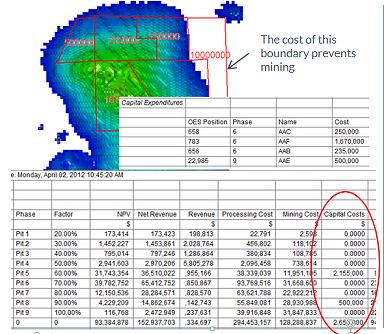
Ultimate Pit optimization can consider boundaries such as property limits and exclusion zones. Costs can optionally be associated with each boundary. The following types of boundaries can be used:
-
Mining must occur within boundaries.
-
Mining must not occur within boundaries.
-
Mining may be avoided within boundaries depending on associated costs and block values.
Reports include summaries of capital costs, for example:
Pit Slopes
A slope model allows you to divide block model volume into three dimensional (3D) Slope Regions. If you do not define slope regions explicitly, the entire block model volume is treated as a single slope region. The number of slope regions is not limited but using small or “thin” volumes as slope regions may result in a loss of slope modelling accuracy. The slope angles within each region can vary with azimuth.
The 3D slope regions can be imported as a field of geological block model or created in your product from 2D outlines and separating surfaces. The outlines can be imported or digitized in Studio NPVS.
The modelling accuracy of slopes within a region is controlled by two slope filter dimension parameters. In most cases the two parameters can be identical. The LG method is sensitive to the values of filter dimensions not exclusively for slope modelling reasons; small values may result in an incorrect ultimate pit, large values may increase the processing time considerably. Experience shows that the slope filter dimensions less than 8 may result in incorrect pits whatever the slope angles.
For example, in a model with cubic blocks, a 45 degree slope angle can be modelled with 1 by 1 slope filter, but because we rely on the LG method we need to use a larger 8 by 8 filter.
Your application helps you choose the right filter dimension parameters with:
-
advice based on block geometry applicable to models with XY square blocks and slope regions with uniform angles in all directions. Studio NPVS presents you with a list of best filters between 8 and 10, fewer than 20, fewer than 30, fewer than 40 and fewer than 50. Keep in mind that large filters require longer Pit Optimizer processing times.
-
A Check Slopes tool that displays modelling errors for any block shapes and any slope definitions.
Defining pit limits
You can restrict ultimate pit to an area within block models in one of two ways:
-
Digitize or import an outline outside which mining is not allowed.
-
Digitize or import outlines inside which mining is not allowed.
You can also import or digitize outlines of areas that can be removed at a cost only in their entirety or not at all. The examples include rivers, railroads, buildings and so on, your product treats the removal costs as capital expenditures and accounts for them in optimization and reporting.
Ultimate Pit and Model Edges
Pit Optimizer does not allow any pit to extend beyond the block model edges defined by vertical planes X=1, X=nX, Y=1, and Y=nY. At the intersections of these planes with the initial topography, the pit can be at most one block deep.
If you import a model that does not define all cells below the initial topography in the nX by nY by nZ rectangular volume, the initial topography along the model edges may be set to the lowest model elevation. In this case, the ultimate pit can go across the boundaries of the solid portion of the model. To avoid this you can define explicit pit limits.
Time Flow and NPV Calculations
Pit Optimizer assumes time flow to be proportional to the tonnage of ore mined. NPV is calculated for OES so the time the 2001st block in the sequence is mined is given by the ore contained in the preceding 2000 blocks.
For example, suppose you set ore mining rate to 1,000,000 tonnes per 365 days, that is, to 2739.726 tonnes per day; and the annual discounting rate to 15% which is equivalent to 0.15/365 daily fractional rate. If the first 2000 blocks in the OES contain 2,342,466 tonnes of ore, the 2001st block is mined on 855th day of mining and its NPV equals its value multiplied by
![]()
= 0.73037
The NPV of the OES is the sum of NPV of its member blocks.
Pit Optimizer NPV is defined as the NPV of Pit Optimizer OES.
Top Down Discounting
The purpose of the Top-Down discounting method is to improve project's NPV by excluding from the ultimate pit ore that could be reached only after mining large amounts of waste. The method is based on the fact that the open pit mining always proceeds from the top down and often waste must be mined before the ore is reached. Since the expenditures on mining waste precede the revenues from mining ore, some deep ore zones may not be worth mining if the time value of money is considered even though they are included in the non-discounted LG ultimate pit.
The Top-Down method uses a procedure based on multiplying block value by a discount factor that is a function of:
- the annual cost of money,
- an estimate of the average annual vertical advance rate of mining, and
- the relative depth of the block.
For example, using a 12% discount rate and an average vertical advance rate of 6 benches per year, the block values should be discounted by 2% (r=0.02); therefore, the discount factor for the kth bench counting from the top of the model is (1/1.02)**k. The values of all blocks at that bench will be multiplied by this factor, whether the block has a negative or positive value.
Note: Top-Down Discounting is a useful heuristic method but it is not guaranteed to improve NPV.
Check Slopes
You can check slope modelling accuracy for selected filter dimensions with Check Values command of Task Pane Optimization screen's Ultimate Pit group. The command generates report that lists maximum possible errors and average errors in the four principal directions for each slope region:
There are three angles considered:
- The slope angle defined in the settings, e.g. 35 degrees.
- Best possible approximation] the best approximation to (1) possible with the given block shapes, say 35.5 degrees.
- The approximation obtained with the slope filter radius defined in the settings, say 36.1 degrees.
The absolute value of the difference between (1) and (2) is in this example 0.6 degrees.
The angles (1) and (2) are measured in all directions (azimuths) for line segments joining centers of the blocks in the model. The differences abs((1)-(2)) may be different for different azimuths. Let’s say they fall between 0.1 and 0.9 and the value 0.9 is obtained at azimuth 183 degrees. Then, the report would say: maximum error is 0.9 degrees at azimuth 183 degrees
The Alternative Underground Method
If at least one processing method is defined as Underground (in Economic Model Settings), you can choose to calculate the ultimate pit to consider the processing cost of the underground vs. open pit method and use the difference in values to determine the ultimate pit.
See Underground Alternative Method.